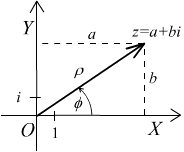Kompleksni broj

Kompleksni brojevi su algebarski izrazi oblika $a+bi$, gdje su $a$ i $b$ realni brojevi, a $i$ imaginarna jedinica koja ispunjava jednadžbu $i^2=-1$.

Zbrajanje, množenje i dijeljenje kompleksnih brojeva zapisanih u obliku uređenih parova definira se formulama:

• $(a_1,b_{1}i)+(a_2,b_{2}i)=(a_1,a_2)+(b_1,b_2)i$
• $(a_1,b_{1}i)(a_2,b_{2}i)=(a_1{a}_2-b_1{b}_2)+(a_1{b}_2+a_2{b}_1)i$

te analogno za oduzimanje i dijeljenje. Motivacija dolazi iz uobičajenih računskih operacija nad realnim brojevima.

U kompleksnom broju $z=a+bi$ broj $a$ se naziva realni dio, piše se $a=Re(z)$, a broj $b$ je imaginarni dio, i piše se $b=Im(z)$.

Kompleksan broj čiji je realni dio jednak nuli naziva se čisto imaginarni broj.

Realni brojevi predstavljaju poseban slučaj kompleksnih brojeva (kad je koeficijent uz $i$ jednak nuli). Iako se kompleksnim brojevima ne izražavaju količine, kao što je to slučaj s realnim brojevima, njihovo uvođenje koristi se u rješavanju problema sastavljenih u terminima realnih brojeva, na primjer, problema o prolazu struje kroz vodič, o profilu krila aviona itd. Kompleksni brojevi izniču u fizici zbog svoje geometrijske prirode (rotacije).

Ništa manje važna nije primjena kompleksnih brojeva na čisto matematičke probleme. Tako na primjer, za određivanje korijena kubne jednadžbe potrebne su operacije s kompleksnim brojevima. Povijesno, kompleksni su brojevi uvedeni radi rješavanja kvadratne jednadžbe. Kvadratna ili bilo koja jednadžba višeg stupnja ako ima kompleksna rješenja, ta će rješenja uvijek doći u konjugiranim parovima - imaginarni dio im je suprotan. Činjenica da kompleksni brojevi ne izražavaju veličine dala je povoda za idealističko tumačenje kompleksnih brojeva (G. Leibnitz). Velika zasluga u smislu materijalističkog tumačenja kompleksnih brojeva pripada L. Euleru. Kompleksni broj se aksiomatski definira kao uređeni par realnih brojeva $(a,b)$. Formule zbrajanja, množenja, dijeljenja se postuliraju ovako:

$(a,b)+(x,y)=(a+x,b+y)$,

$(a,b)\cdot (x,y)=(ax-by,ay+bx)$,

$\frac{(a,b)}{(x,y)}=(\frac{ax+by}{x^2+y^2},\frac{bx-ay}{x^2+y^2})$.

Par $(0,1)$ se naziva imaginarna jedinica i označava simbolom $i$. Iz potonjih formula slijedi da je $i^2=-1$. Operacije nad kompleksnim brojevima zadovoljavaju obične zakone komutativnosti, distributivnosti i asocijativnosti (kao i u slučaju realnih brojeva). Međutim, operacije nad kompleksnim brojevima pod radikalima (korijenima) donekle se razlikuju od analognih operacija s realnim brojevima. Tako je

$-1=i^2=\sqrt{-1}\cdot \sqrt{-1}=\sqrt{(-1)(-1)}=1$.

Trigonometrijski oblik

Ponekad je kompleksne brojeve pogodno pisati u trigonometrijskom obliku:

$a+bi=\rho (\cos \varphi +i\sin \varphi )$,

$\rho =\sqrt{a^2+b^2},\varphi =\arctan \frac{b}{a}$, za $a>0$ i $\varphi =\pi +\arctan \frac{b}{a}$ za $a<0$; kada je $a=0$ onda je $\varphi =\frac{\pi }{2}$, ako je $b>0$ i $\varphi =-\frac{\pi }{2}$, ako je $b<0$. Broj $\rho$ se naziva modul kompleksnog broja, a $\varphi$ je argument kompleksnog broja. Množiti kompleksne brojeve je vrlo pogodno baš u ovom obliku: u množenju kompleksnih brojeva množe se njihovi moduli, a argumenti se zbrajaju. Iz ovog pravila proizlazi De Moivreova formula:

$(\cos \varphi +i\sin \varphi {)}^n=\cos n\varphi +i\sin n\varphi$ .

Kompleksni se brojevi često predstavljaju vektorima u kompleksnoj ravnini (slika dolje). Geometrijski smisao brojeva $a,b,\rho ,\varphi$ vidi se na crtežu. U zbrajanju kompleksnih brojeva njihovi vektori se zbrajaju po tzv. pravilu paralelograma.

Duljina vektora $\rho$ je modul kompleksnog broja, a kao što se vidi na gornjoj slici, može se dobiti pomoću Pitagorinog poučka. Modul, intenzitet kompleksnog broja često označavamo kao apsolutnu vrijednost, tj. udaljenost broja od ishodišta koordinatnog sustava: $|z|=\rho =\sqrt{a^2+b^2}$.

Kompleksni brojevi u trigonometrijskom obliku su usko povezani s eksponencijalnom funkcijom imaginarnog argumenta. Vrijedi sljedeća Eulerova formula:

$e^{i\varphi }=\cos \varphi +i\sin \varphi$;

preko nje se definira stupnjevanje kompleksnih brojeva, logaritam kompleksnog broja i dr.

Kompleksni brojevi oblikuju algebarski zatvoreno polje. Polje kompleksnih brojeva je proširenje polja realnih brojeva pridruživanjem ovom polju elementa $i$, takvog da je $i^2=-1$.

Zanimljivosti

Kako je egzistenciju kompleksnih brojeva kroz povijest pratio određeni skepticizam, veliki njemački matematičar, koji je samostalno otkrio geometriju kompleksnih brojeva, Carl Friedrich Gauss, u jednom je pismu napisao:

To što je ova tema [imaginarni brojevi] do sada bila okružena tajanstvenom nejasnoćom, uglavnom se može pripisati loše prilagođenom zapisu. Da su se, na primjer, +1, -1 i kvadratni korijen iz -1 nazivali izravnim, inverznim i bočnim jedinicama, umjesto pozitivnim, negativnim i imaginarnim (ili čak nemogućim), takva nejasnoća ne bi dolazila u obzir.