Stirlingov ciklus

Stirlingov ciklus ili proces je termodinamički kružni ciklus po kojem rade Stirlingovi uređaji. Ciklus i uređaj koji radi po njemu su osmislili i patentirali braća Robert Stirling, svećenik, i James Stirling, inženjer, 1816. godine. Kako je riječ o termodinamičkom kružnom ciklusu, to znači da se ciklus vodi između dva toplinska spremnika različitih temperatura, tj. između ogrjevnog i rashladnog spremnika, a ukupna izmijenjena toplina između toplinskih spremnika jednaka je ukupnom izvršenom mehaničkom radu. Stirlingov ciklus može biti desnokretan ili lijevokretan; ako je desnokretan, mehanički rad se dobiva te uređaj radi kao motor, a ako je lijevokretan, mehanički rad se troši te uređaj radi kao rashladni uređaj ili dizalica topline. Specifičnost Stirlingovog ciklusa u odnosu na ostale kružne procese je taj što osim što je teoretski izveden kao zatvoren sustav, tako je izveden i u tehničkoj praksi; to znači da uređaji koji rade na principu Stirlingovog ciklusa nemaju usis i ispuh i da je unutar sustava sadržana konstantna masa radne tvari. Ciklus se u osnovi sastoji od dvije izoterme i dvije izohore.

Teorijski Stirlingov ciklus

Primjer motora koji radi na principu desnokretnog zatvorenog Stirlingovog ciklusa; u ovom slučaju Stirlingovog motora ß - tipa.

Teorijski desnokretni Stirlingov ciklus u p,v i T,s - dijagramu.

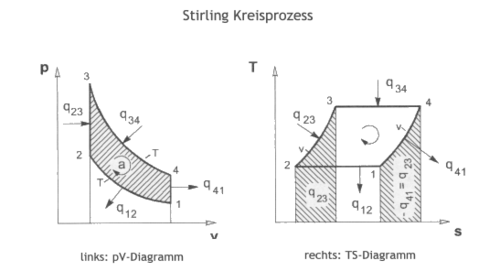
Teorijski Stirlingov ciklus razmotrit će se kao desnokretni zatvoreni ciklus; ciklus se sastoji od četiri promjene stanja:

• 1-2: izotermna kompresija - rashladni spremnik odvodi toplinu radnom mediju zbog čega se radnom mediju smanjuje volumen
• 2-3: izohorno dovođenje topline - stlačeni radni medij prolazi kroz regenerator koji ga grije dovodeći mu toplinu pri konstantnom volumenu
• 3-4: izotermna ekspanzija - ogrjevni spremnik dovodi toplinu radnom mediju povećavajući mu volumen
• 4-1: izohorno odvođenje topline - radni medij se vraća kroz regenerator predajući mu toplinu pri konstantnom volumenu.

Dok se na jednom dijelu cilindra izvode promjene stanja 2-3 i 3-4, na drugom dijelu cilindra se izvode promjene stanja 4-1 i 1-2 i obratno.

Energijska analiza Stirlingovog ciklusa

Specifična toplina se dovodi pri promjenama stanja 2-3 i 3-4:

$q_{23}=c_v\mathrm{\Delta }{T}_{23}=c_v(T_3-T_2)>0[J/kg]$

$q_{34}=T_{max}\mathrm{\Delta }{s}_{34}=T_{max}Rln\left(\frac{v_4}{v_3}\right)>0[J/kg]$

gdje je $q$ - specifična toplina, $c_v$ - specifični toplinski kapacitet pri konstantnom volumenu, $T$ - termodinamička temperatura, $s$ - specifična entropija, $R$ - individualna plinska konstanta, $v$ - specifični volumen. Ukupno dovedena specifična toplina iznosi:

$q_{dov}=q_{23}+q_{34}>0[J/kg]$ .

Specifična toplina se odvodi pri promjenama stanja 4-1 i 1-2:

$q_{41}=c_v\mathrm{\Delta }{T}_{41}=c_v(T_1-T_4)<0[J/kg]$

$q_{12}=T_{min}\mathrm{\Delta }{s}_{12}=T_{min}Rln\left(\frac{v_2}{v_1}\right)<0[J/kg]$ .

Ukupno odvedena specifična toplina iznosi:

$q_{odv}=q_{41}+q_{12}<0[J/kg]$ .

Kako je ukupno dobiveni specifični rad $w_{uk}$ jednak ukupno izmijenjenoj specifičnoj toplini:

$w_{uk}=q_{dov}-\left|q_{odv}\right|$ ,

iz toga slijedi:

$w_{uk}=q_{23}+q_{34}-|q_{12}+q_{41}|$

$w_{uk}=c_v(T_3-T_2)+T_{max}Rln\left(\frac{v_4}{v_3}\right)-[T_{min}Rln\left(\frac{v_1}{v_2}\right)+c_v(T_4-T_1)]$.

U gornjoj jednadžbi su zamijenjena mjesta temperaturama $T_4$ i $T_1$ te specifičnim volumenima $v_1$ i $v_2$ jer se predznakom - uz veličinu $q_{odv}$ već naglasila činjenica da se radi o odvedenoj toplini. Kako se proces izvodi regenerativno, izohorno dovedena i izohorno odvedena specifična toplina su teorijski jednake, ali suprotnih predznaka tako da se one poništavaju. Još se može primijetiti da su $v_1=v_4$ i $v_2=v_3$ iz čega se zaključuje da su $\mathrm{\Delta }{s}_{12}=\mathrm{\Delta }{s}_{34}$ te iz tih spoznaja slijedi:

$w_{uk}=T_{max}Rln\left(\frac{v_4}{v_3}\right)-T_{min}Rln\left(\frac{v_4}{v_3}\right)$

$w_{uk}=(T_{max}-T_{min})Rln\left(\frac{v_4}{v_3}\right)>0[J/kg]$

Gornja relacija predstavlja ukupno dobiveni specifični rad ciklusa, a ako ga se pomnoži s ukupnom masom radnog medija, tada se dobije ukupno dobiveni rad desnokretnog zatvorenog teorijskog Stirlingovog ciklusa. Snaga stroja koji bi radio na principu teorijskog Stirlingovog ciklusa $P_S$ glasi:

$P_S=w_{uk}{m}_{uku}n>0\left[W\right]$

gdje je $m_{uku}$ - ukupna masa radnog medija, a $n$ - broj okretaja stroja u sekundi.

Termički stupanj djelovanja Stirlingovog ciklusa

Termički stupanj djelovanja Stirlingovog ciklusa se definira kao:

${\eta }_S=\frac{w_{uk}}{q_{34}+(1-{\eta }_{reg})q_{23}}$ ,

a kako je u teorijskom ciklusu regenerator idealan ( ${\eta }_{reg}=1$ ), tada vrijedi:

${\eta }_S=\frac{w_{uk}}{q_{34}}=\frac{(T_{max}-T_{min})Rln\left(\frac{v_4}{v_3}\right)}{T_{max}Rln\left(\frac{v_4}{v_3}\right)}$ .

Konačno,termički stupanj djelovanja teorijskog Stirlingovog ciklusa glasi:

${\eta }_S=\frac{T_{max}-T_{min}}{T_{max}}$ .

Usporedba s ostalim teorijskim kružnim ciklusima

Teorijski Stirlingov ciklus s idealnim regeneratorom prema termičkom stupnju djelovanja potpuno je ekvivalentan termičkom stupnju djelovanja Carnotovog (najveći termički stupanj djelovanja) i Ericssonovog ciklusa (Ericssonov ciklus postiže Carnotov termički stupanj djelovanja samo uz idealni regenerator kao i Stirlingov ciklus), a veći od termičkog stupnja djelovanja Jouleovog, Dieselova i Ottova ciklusa. Prema dobivenom radu, najbolji ciklus je Ericssonov, a zatim slijede Stirlingov, Jouleov, Dieselov, Ottov te Carnotov ciklus.

Realni Stirlingov ciklus

Realni desnokretni Stirlingov ciklus - utjecaj gibanja klipa na količinu dobivenog rada; lijevo: sinusoidno gibanje, desno: diskontinuirano gibanje.

Nijedan današnji stroj ne radi na principu teorijskog kružnog ciklusa pa tako ni na principu teorijskog Stirlingovog ciklusa; razlozi su sljedeći: loše brtvljenje, postojanje volumena štetnog prostora, trenje, regeneratori koji nisu idealni... Unatoč tomu, možemo približno opisati tok Stirlingovog ciklusa uzimajući u obzir određene nesavršenosti te se tako dobije realni Stirlingov ciklus.

Izvori

Stirlingov motor [1]
Stirling cycle [2]
Stirling-Kreisprozess [3]
Predložak:Izvori